雑文
ナップサック問題は解きやすい?
昨年度から情報・電気・数理データサイエンス系入門という1年生向けのガイダンス科目を複数名の教員で担当しています.私は2コマ(1コマは50分)を使って情報工学コースの概要を紹介しており,その中で,計算機に問題を解かせるとはどういうことか,計算機にとって解きやすい問題と解きにくい問題の境界はどこか,について解説しています.
ほとんどの1年生は計算機やプログラミングに関する予備知識をもっていないので難しい話をすることはできません.難しい話をして情報工学コースへの希望者が減るのも避けたいところです.そこでまず,メモリ・CPU・プログラムをそれぞれ箱・代理人・指示書に置き換え,100個の箱に入った100個の整数の最大値を求める問題や,100個の箱に入った100個の整数を小さい順に並べ替える問題を示し,これらを代理人に解いてもらうためにはどのような指示書を作成すればよいかを考えてもらいます.次に,計算機にとって解きやすい問題とそうでない問題の違いを説明します.具体的には,入力の長さの多項式回のステップで代理人の作業が終了するような指示書が存在する問題は解きやすく,そのような指示書が見つかっていない問題は解きにくいと伝えます.上記の二つはいずれも,適切な指示書の下で代理人の作業が入力の長さの多項式回のステップで終了しますので解きやすい問題といえます.その後,解きにくい問題の例として巡回セールスマン問題を取り上げ,単純な解法では,都市数から1を引いた数の階乗通りの巡回路の長さをしらみつぶしに調べる必要があることを示します.また,解きにくい問題の代表例として,充足可能性問題,ハミルトン閉路問題,部分和問題,ナップサック問題が広く知られていることを伝えます.最後に,解きやすい問題と解きにくい問題の関係を明らかにすることは計算機科学の重要な未解決問題であり,クレイ数学研究所が2000年に発表したミレニアム問題の一つとして100万ドルの懸賞金が掛けられていることを説明します.
先日の講義終了後に受講生のA君(情報・電気・数理データサイエンス系1年生)から「ナップサック問題は動的計画法を用いて簡単に解けるのに,なぜ解きにくい問題に含まれているのでしょうか」との質問を受けました.1年生からそのような質問が出ることに驚きましたが,詳しく聞いてみると,入学前からアルゴリズムに興味があって自分で勉強していたそうです.
ナップサック問題とは,重量と価値が分かっているn種類の品物の中からいくつかを選び,重量制限Wを超えない範囲でナップサックに詰め込み,ナップサック内の品物の価値の総和を最大にせよというものです.以下では,i番目の品物の重量と価値をそれぞれwi, viで表し,これらと重量制限Wはすべて正の整数であると仮定します.さらに,ナップサックに詰め込む品物を1番目からi番目までに制限して重量制限を0以上W以下の整数wとしたときの品物の価値の総和の最大値をV(i,w)で表し,便宜上V(0,0)=V(0,1)= … =V(0,W)=0と定義します.このとき,V(i,w)はwiがwよりも大きければV(i-1,w)に等しく,wiがw以下であればV(i-1,w)とV(i-1,w-wi)+viの大きい方に等しいことがわかります.これを利用すると,最初にV(1,0), V(1,1), … , V(1,W)の値が定まり,次にV(2,0), V(2,1), … , V(2,W)の値が定まり,最後にV(n,0), V(n,1), … , V(n,W)の値が定まります.V(n,W)の値がナップサック問題の解であり,この計算過程を逆にたどればナップサックに詰め込む品物も決まります.これが動的計画法を用いたナップサック問題の解法です.
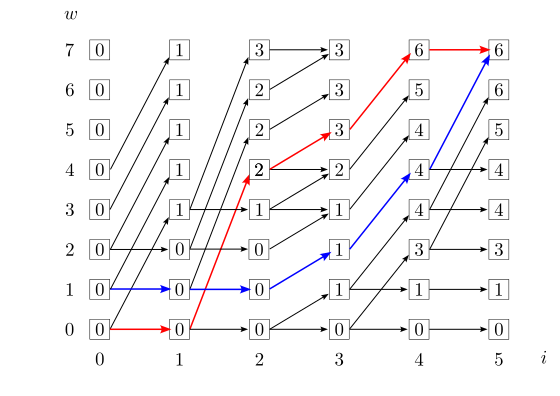
例えば,5種類の品物の重量と価値が,w1=3, v1=1, w2=4, v2=2, w3=1, v3=1, w4=2, v4=3, w5=3, v5=2で与えられ,重量制限がW=7のときのナップサック問題を動的計画法を用いて解くと下図のようになります.四角の中の整数がV(i,w)の値を表しており,矢印はその値がV(i-1,w)とV(i-1,w-wi)のどちらから得られたのかを表しています.矢印が左隣の四角から来ているのであればi番目の品物は詰め込まない(価値が変化しない)ことを意味し,左下の四角から来ているのであればi番目の品物を詰め込む(価値がviだけ増加する)ことを意味します.この図より,価値の総和の最大値はV(5,7)=6であることがわかります.また,赤い矢印と青い矢印を逆に辿ることにより,詰め込む品物の組み合わせは4,3,2と5,4,3の二通りあることがわかります.
A君の質問の意図は「ナップサック問題は動的計画法を用いればnW回のステップで解けるのになぜ解きにくい問題なのか」です.この質問に答えるには,問題の「入力の長さ」の厳密な定義を考慮する必要があります.計算機の中ではすべての数が2進数で表されるので,例えば100個の整数の最大値を求める問題の場合,入力の長さは各整数を2進数で表すのに必要なビット数を100個の整数分集めたものになります.しかし,講義の中では説明を簡単にするために入力の長さは100であると述べました.これがA君の混乱を招いた原因かもしれません.ナップサック問題の入力の長さはどうでしょうか.重量と価値を2進数で表すのに必要なビット数をn品物分集めたものと重量制限Wを2進数で表すのに必要なビット数の和になります.議論を簡単にするために,各品物の重量と価値はあわせてbビットの2進数で表されると仮定します.すると入力の長さはL=bn+log2Wとなります.これよりW=2L/2bnが得られますので,動的計画法を用いたナップサック問題の解法のステップ数はnW=n2L/2bnとなります.しかし,2LはLの多項式ではありませんので,ナップサック問題は解きやすいと結論付けることはできません.
A君から質問を受けたときは,予想外の質問に慌ててしまい,きちんと回答することができませんでした.この文書がA君の目に留まり,私の説明に納得してくれることを祈ります.
(2022/6/6公開)
久しぶりの対面講義
今学期の制御論は,直後の実験科目が対面で行われることを考慮し,対面形式とオンライン形式(Microsoft Teamsによるライブ配信)を同時に併用しています.最後に対面で講義を行ったのが2020年12月21日の数理計画特論ですから,およそ9か月半ぶりの対面講義です.幸か不幸か制御論は受講者がそれほど多くありませんので,当初は対面形式のみで実施することを考えていましたが,講義室での受講を望まない学生もいると思い,最終的にライブ配信も同時に行うことにしました.CONNECT(京都大学高等教育研究開発推進センターが制作・運用しているサイト)によると,この方式はハイフレックス型授業とよばれており(恥ずかしながらこれを書くまで知りませんでした),利点は学生が対面とオンラインを選択できることや完全オンラインへの移行が容易であること,欠点は教室環境の設定が大変であることや教員の負荷が高いことだそうです.
制御論を行う工学部第11講義室には黒板,プロジェクタ,スクリーンが設置されており,ノートPCを持参すればWi-Fiでインターネットに接続することもできます.しかし,遠隔講義用の特別な設備はありません.この状況でどのようにして板書講義をオンライン化するか検討した結果,2台のウェブカメラで黒板の左半分と右半分を撮影してそれらを切り替えながらライブ配信することにしました.ウェブカメラの台数は増えますが,これなら第2学期までとほぼ同じやり方で講義を行うことができます.早速ウェブカメラ1台とUSB延長ケーブル2本を購入し,既存のウェブカメラ1台,USBマイク,ノートPCと一緒に講義室に持ち込んでテストしてみました.心配だったのは板書がどの程度鮮明に映るかという点でしたが,ウェブカメラを適切な位置に設置してピントを合わせれば,まったく問題ありませんでした.むしろホワイトボードの字よりも見やすい印象を受けました.新たに購入したウェブカメラは既存のそれと同じくマニュアルフォーカスですが,画角が広かったりフレームレートが高かったりと仕様が異なっています.この点も少し心配していましたが,画質や歪み度合いが少し異なるぐらいで大きな問題ではありませんでした.
講義初日,余裕を見て開始時刻の約30分前に講義室に入り,ノートPC, ウェブカメラ,USBマイク,小型スピーカー等の機器の設置を行いました.この日は板書に加えてPID制御のデモ動画を見せる予定でしたので,講義室で受講する学生のために小型スピーカーも必要でした.初めてということもあって予想以上に作業に手間取り,教室環境の設定が大変であるというハイフレックス型授業の欠点を実感しました.それでも何とか開始時刻の約10分前には準備が完了し,それからTeamsで会議を起ち上げて予定通りに講義を始めることができました.直後の実験科目が対面で行われることから大半の学生が対面を選択すると予想していましたが,講義室に来たのは半数未満で残りはTeamsの会議に参加していました.オンライン形式を併用するのは正しい判断だったようです.
初回の講義は大きな問題もなく無事に終了しました.久しぶりに学生の反応を見ながら説明できたので充実感がありましたが,それと同時に,Teamsの会議に参加した学生の多さからオンライン形式の重要性も再認識しました.2回目の講義でもオンラインを選択した学生の人数は初回とほとんど変わりませんでしたので,オンラインでもある程度の満足感は得られているのではないかと思います.今回採用した方法には,2台のウェブカメラ,マイク,2本のUSB延長ケーブル,2個の三脚が必要ですが,高価なものは一つもなく3万円以下ですべてを揃えることができます.したがって板書講義を低コストでオンライン化することが可能です.その一方で,毎回これらの機器を講義室に持ち込んで設定しなければならないのは大きな課題です.これから対面形式とオンライン形式を併用した講義が増えてくると思います.私の経験が少しでも参考になれば幸いです.



(2021/10/9公開)
キャンパス内の小動物
数日前の午後8時頃,キャンパス内のバイク置き場に4匹の小動物がいるのを見つけました.以前にも似たような動物がキャンパス内の側溝でもぞもぞしているのを見たことがありますが,蛍光灯に照らされた明るい場所で,しかも群れでいるのを見たのは初めてでした.4匹のうちの2匹はじゃれ合って遊んでいるようでした.珍しい光景なので記録に残しておこうと思い動画撮影を行いましたが,その間も小動物たちは逃げる気配を見せず,バイク置き場をうろうろしていました.近くを自転車で通りがかった外国人の方もペダルを止め,しばらく二人で一緒に小動物たちを眺めました.
帰宅後,その動画を妻に見せると,妻は「ハクビシンの可能性があるから大学に報告して対策してもらった方がいいのではないか」と言います.近くの空き家にハクビシンが住みついているかもしれないという話を隣人から最近聞いたそうです.インターネットでハクビシンや似たような動物の画像や動画を閲覧してみましたが,動物に疎い私には特定することができませんでした.
翌日,専門家に見ていただくのがよいと思い,岡山理科大学理学部動物学科の中本敦先生にメールを送りました.中本先生との面識はありませんでしたので反応がないことも覚悟していましたが,その日のうちに大変丁寧な返信を頂きました.小動物はイタチ科の二ホンアナグマ(Meles anakuma)とのことです.普段は半田山に住んでいて,側溝の中を移動しながら時々住宅地に現れているそうです.ということは,私が側溝で見たのもおそらく二ホンアナグマでしょう.基本的にはおとなしい性格で,触らない限り攻撃してくることはなく,少し音を立てるとびっくりして逃げていくそうです.近くで撮影できたのは運が良かったのかもしれません.噛まれない限り病気等も気にしなくてよく,特別な対策も必要ないので,やさしく見守ってくださいとのことでした.岡山大学では現在,新型コロナウイルス感染拡大のため活動制限レベルが3に引き上げられており,キャンパス内に学生の姿はほとんどありません.早く活動制限が解除されて,自然豊かな津島キャンパスに学生の皆さんが戻ってくることを願っています.
(2021/6/16公開)
解答用紙の裏
大学院生の頃,ある専門学校で英語の授業を行う非常勤講師のアルバイトをしました.研究室の先輩から後任を探しているという話を聞いたのがきっかけでした.英語が得意という訳ではありませんでしたが,情報処理技術に関連する英単語や英文に特化した内容だから大丈夫と先輩に説得され,一年間の予定で引き受けることにしました.家庭教師の経験が多少はありましたし,教えることも嫌いではありませんでしたので,何とかなるだろうと思っていました.
最初の授業の日,40人以上の女子学生で一杯の教室に入った途端,理系大学院生の普段の生活とは全く異なるその雰囲気に圧倒されてしまいました.そこから先の記憶がほとんどありません.おそらく大粒の汗を流しながら要領の悪い説明を繰り返していたことと思います.緊張は学生達にも容易に伝わっていたはずです.残念ながら家庭教師の経験はほとんど役に立ちませんでした.
二度目の授業以降もしばらくは同じような状況が続きましたが,学生達が気さくに接してくれたおかげで徐々に雰囲気に慣れてきて,授業の進行や学生達とのコミュニケーションも少しずつうまくできるようになりました.いつの間にか一週間に一度の異空間は私の楽しみになっていました.しかし楽しい時間は速く過ぎるものです.あっという間に一年が過ぎ,寂しさを覚えつつも研究室の後輩にバトンタッチしました.
それから四半世紀以上が経ちました.私の生活にもいくつかの大きな変化があり,現在では,専門学校のあった場所から遠く離れた街で家族と暮らしています.専門学校は名前も所在地も変わったようです.当時の学生達もそれぞれの人生を歩んでいることと思います.
先日,専門学校の期末試験の解答用紙を数年ぶりに広げました.少し変色した解答用紙の裏には学生達からのメッセージが書かれています.クラスの誰かが計画し,全員で協力して実行したのでしょう.新米の非常勤講師を暖かく迎えてくれ,最後にこのような贈り物をしてくれたことに感激しました.若かりし頃のこの出来事は今でも心に強く残っています.
(2021/1/19公開)
Microsoft Teamsによるオンライン講義
数年前から第2学期に情報系学科3年生を対象にした応用線形代数という講義を担当しています.今年度は新型コロナウイルス感染症の影響でこの講義をオンラインで行うことになりました.昨年度までの対面講義は板書形式で行っていましたので,どのような形にするかでかなり悩みました.講義ノートは多くの数式で埋め尽くされているためスライドを作成するのは大変そうでしたし,何よりスライドでは教えるペースが速くなってしまうおそれがありました.事前に動画を撮影しておいてアップロードすることも考えましたが,誰も聞いていない中で説明するのは気が進みませんでした.
昨年度までのやり方にできるだけ近い形を模索した結果,ホワイトボードに板書しながら説明する様子をウェブカメラで撮影し,それをMicrosoft Teamsでライブ配信する方法に落ち着きました.また,ライブ配信と同時に録画を行い,動画ファイルをMicrosoft Streamにアップロードして学生が講義後に視聴できるようにしました.利用した機器はWindows10搭載のノートPC,手動フォーカスのウェブカメラ,USBマイクです.カメラには三脚を取り付けてホワイトボード全体が写る位置に置き,焦点をホワイトボードに合わせました(幸い私の研究室には壁に固定されたホワイトボードがあります).実を言うと,講義開始日の二週間ほど前に研究室の4年生のゼミでオートフォーカスのカメラを試してみたのですが,私に焦点が合ってしまってホワイトボードの文字がぼやけるという問題が判明したため,急遽,手動フォーカスのカメラを購入しました.価格は5,000円前後だったと思います.
講義の各回の流れは次の通りです.講義開始前にTeamsとWindows10のカメラアプリケーションを同時に起動し,TeamsではノートPCのカメラを,カメラアプリケーションではウェブカメラを選択しておきます.講義開始時にはノートPCの前に座り,Teamsのビデオをオンにして前回の演習問題の解説やその日の講義内容の概要説明を行います.次に,Teamsでカメラアプリケーションのウィンドウを画面共有し,カメラアプリケーションで録画開始ボタンをクリックしてから板書を始めます.これらの操作は忘れやすいので注意が必要です.実際,操作を忘れたまま板書を始めてしまい,学生から指摘されたことが何度かありました.板書による講義は対面講義と同じ要領で行いますが,目の前には誰もいませんのでウェブカメラに向かって説明します.この点は最後まで慣れませんでした.ホワイトボードが板書で一杯になったらカメラアプリケーションの録画停止ボタンをクリックし,写真撮影モードに切り替えてホワイトボードの画像を撮影します.また,このタイミングで学生達に質問がないか確認します.あとはこの繰り返しです.一回の講義で画像約10枚と動画約10本ができます.講義終了後,画像はTeamsにアップロードし,動画はフリーソフトFFmpegで圧縮してからMicrosoft Streamにアップロードし,Teamsで視聴できるようにしました.
今回の講義では,学生からTeamsのチャット機能で質問や板書間違いの指摘が何度かありました.板書に間違いがあった場合は少々面倒です.カメラアプリケーションを録画モードに切り替えて再び録画を開始し,板書の修正をしながら説明を行い,最後に録画を停止してホワイトボードの画像を撮影します.また,講義終了後には,間違った板書や説明を含んでいる動画とそれを訂正している動画を一本にまとめる作業が必要です.間違った説明で完結してしまう動画によって学生達の誤解を招かないようにするためと,画像と動画を一対一に対応させるためです.
試行錯誤しながら行った初めてのオンライン講義は7月末に無事終了しました.第1学期と第2学期のオンライン講義に関する学生アンケートで何人かの学生から「応用線形代数の講義がよかった」とのコメントをもらいましたので,今回のやり方は概ね成功だったようです.教える側にとっても,教室での板書による講義とほとんど同じ要領でできることや,講義の様子が動画の形で記録されることなど,いい面がいくつかあります.この講義では全部で129本の動画ができました.各動画の再生回数は多くありませんでしたが,これはライブ配信が予想以上にうまくいったからと勝手にいい方に解釈しています.
これまでずっと板書形式で講義をやってこられてオンライン講義もできるだけそれに近い形でやりたいとお考えの方は少なくないと思います.ここで書いたことが少しでも参考になれば幸いです.

(2020/8/13公開)
在宅勤務
岡山大学では4月17日に新型コロナウイルス感染拡大防止のための活動制限指針が示されました.それ以前から学部生の登校は禁止されていましたが,大学院生の登校も禁止になり,教員の研究室での活動についても,オンライン授業のための必要最低限の立ち入り以外は原則禁止になりました.私自身は1学期に授業を担当していないため,必然的に在宅勤務になりました.
在宅勤務への移行が決まった日,研究室の4年生のゼミをどうするかで悩みました.私の研究室では毎年4月から7月にかけて週に2回のペースで4年生と洋書の輪読を行っています.昨年までは,大きなホワイトボードが備え付けられた部屋に参加者全員が集まり,口頭による説明で不十分な場合にはホワイトボードに数式や図を書いたりして議論を深めていました.今年はオンラインで開催することになり当初は不安がありましたが,私がホワイトボードに数式や図を書いて説明し,それをウェブカメラで映して自宅や下宿先にいる学生に見せるようにしたため,これまでと近い形で進めることができていました.しかし,在宅勤務になるとそうはいきません.
ゼミが明日に迫っていたので,岡山駅近くのホームセンターに行って壁掛けタイプのホワイトボードと洗濯物干しとS字フックを購入し,即席の脚付きホワイトボードを作りました.自室の構造の関係で脚付きタイプのホワイトボードが欲しかったのですが,店内にあったのは壁掛けタイプのみで,脚付きタイプは取り寄せに一週間掛かるとのことでした.ホワイトボードが固定されていないため書くときに少しガタガタするのが難点ですが,それを除けばまったく問題ありません.出費も脚付きホワイトボードを買うよりもかなり安く抑えられました.
翌日のゼミで早速ホワイトボードを利用しました.デスクトップPCのディスプレイにウェブカメラを取り付け,私の背後にホワイトボードを置き,必要に応じて数式などを書いて説明しました.学生にどの程度はっきり見えているのか正確にはわかりませんが,ホワイトボードを見て学生達は納得していましたので,問題ないのだろうと思います.
現在,大学の研究教育活動には様々な制約があります.教員はその中でできることをやっていくしかありません.新型コロナウイルス禍が一刻も早く収まり,学生達の活気溢れる賑やかなキャンパスが戻ってくることを切に願いつつ,自宅で即席のホワイトボードセットを使ったゼミを続けていきます.

(2020/4/25公開)
学科長からのメッセージ
世界中で新型コロナウイルスが猛威を振るっています.これを書いている3月30日現在,日本で感染爆発は起こっていないものの,感染者数は日に日に増加しています.感染拡大を防ぐため,ほぼすべての小中学校と高等学校は3月3日から休校措置をとっていますし,多くの企業は出張自粛や在宅勤務などの取組みを行っています.岡山大学でも,3月25日の卒業式と4月2日の入学式が中止になり,新年度の授業開始も4月20日に延期されました.
ウイルス終息のために医学や薬学の発展が必要なのは言うまでもありませんが,情報技術の役割も小さくありません.実際,企業の在宅勤務を可能にしているのはインターネット,グループウェア,Web会議システムなどの情報技術です.採用活動のための会社説明会や面接もWeb会議システムで行われています.一方,自宅で過ごす小中学生や高校生は,インターネット上の動画を見たり,SNSで友達と情報交換したり,オンラインゲームをしたりして楽しんでいます.また,国外に目を向けると,台湾では薬局のマスクの在庫状況を把握するためのアプリが,韓国では自宅隔離中の市民の行動を管理するアプリが利用されています.情報技術には解決すべき課題も多くありますが,私達の生活を守るための社会基盤として,今後ますます重要になるでしょう.
情報系学科では,そのような社会基盤を支える技術者や研究者を目指す学生達が,情報技術の基礎から応用までを学んでいます.数学,情報と計算の理論,データ構造とアルゴリズム,コンピュータのソフトウェアとハードウェア,プログラミング,音声・画像・自然言語の処理,人工知能,情報ネットワーク,データベース,セキュリティなどに関する講義・演習・実験を通して基礎学力と実践力を身に付けています.また,卒業生の6割以上が大学院に進学し,最先端の研究を推進しています.
情報の分野では新しい技術やアイデアが次々に生まれています.それらが社会生活を大きく変えることもあります.安心安全かつ便利で豊かな社会の実現に向けて,私たちと一緒に情報技術の未来を拓きましょう.
(2020/3/30公開)
ブラックモンブラン
岡山大学生協のピオーネショップにはブラックモンブランがあります.これは佐賀県にある竹下製菓が製造しているアイスで,九州では知らない人はいないほど有名です.どのコンビニやスーパーでも購入できます.熊本生まれの私も小さい頃から大好きです.
2019年の7月だったでしょうか.ピオーネショップのアイス人気投票でブラックモンブランが1位になりました.岡山ではあまり知られていない九州生まれのアイスが岡大生に愛されていることを知って嬉しくなり,その日の帰宅後,同じ九州出身の妻にそのことを伝えました.それからしばらくして,ブラックモンブラン誕生50周年を記念して竹下製菓が「思い出のエッセイコンテスト」を実施していることを妻から聞きました.ちょうどお盆休みの最中でしたので,私とブラックモンブランの関わりや人気投票のことをエッセイにまとめて応募しました.結果は残念ながら落選でしたが,論文と同じで誰にも読まれず消えていくのは悲しいので,恥を忍んでここに掲載します.
ブラックモンブラン熊本の実家近くの駄菓子屋にはいつもブラックモンブランがあった。当時は五十円だったと思う。小学生の私は日曜日になると百円玉を持って出掛け、日が暮れるまで近所の友達と缶蹴りや野球をして遊んだ。遊びの合間にみんなで駄菓子屋に行ってお菓子を買うのだが、お小遣いの半分を一気に使うのは贅沢に感じられ、安いお菓子ばかり買っていた。たまにしか買えないブラックモンブランは高級品であった。
それから約二十年後、福岡で仕事に就き家庭も築いた私は、子供の頃の反動か、頻繁にブラックモンブランを買った。昔と変わらず美味しかった。コンビニのレジにブラックモンブランを持っていく際の気恥ずかしさはあったが、それに勝る美味しさがあった。しょっちゅう買うものだから当たり棒も集まり、何度もブラックモンブランと交換したし、クオカードも二回ほど頂いた。
六年ほど前から家族と岡山で暮らしている。転居後間もなく、この地域のコンビニやスーパーにブラックモンブランがないことを知った。見知らぬ土地に来たことを改めて実感し、寂しさを覚えた。そんな中、勤務先の大学の売店でブラックモンブランを見つけた。それ以来、学生の目が気になって買えないものの、売店に行く度に横目でその存在を確認している。先日、その売店のアイスクリーム人気投票でブラックモンブランが1位になった。幼馴染みが同じ土地で頑張っているようで嬉しかった。久しぶりにブラックモンブランを食べたくなった。
大賞作品や入選作品は竹下製菓のウェブページに掲載されています.どれもアイスの思い出が情景豊かに書かれていて素晴らしいと思うとともに,九州の人達のブラックモンブラン愛を再認識しました.
(2019/12/29公開,2021/6/18リンク修正)
自然数の集合は非可算?
昨年度から「工学安全教育」という講義の一部を担当しています.私の担当部分の主要テーマは「ソフトウェアの万能性と自動化の限界」であり,ソフトウェアは万能でないということを停止性判定問題を通して説明します.その中で対角線論法を用いるのですが,本日の講義終了後に受講生のA君(情報系学科1年生)から「対角線論法を用いると自然数の集合が非可算であるということが証明されてしまいます.この証明のどこが間違っているのでしょうか?」という質問を受けました.A君の証明は以下の通りです.
【A君の証明】各自然数の最上位桁の左には見えない0が無限個並んでいると考え,各自然数を0,1,...,9の無限列に変換します.例えば231は...0000231に変換されます.いま,自然数の集合は可算であると仮定すると,これらの無限列には1,2,3...と番号をつけることができます.そこで
...000001 : 1
...000002 : 2
...000003 : 3
...
と番号をつけることにします.このとき,右端の数字が2でその他の数字がすべて1である無限列...111112を考えます.この無限列と上の表の1行目の無限列を比べると右端の数字が異なるので両者は等しくありません.また,この無限列と上の表の2行目の無限列を比べると右から2番目の数字が異なるので両者は等しくありません.以下同様に,無限列...111112は上の表のどの無限列とも等しくありません.これは番号のつかない自然数が存在することを意味しています.したがって自然数の集合は非可算です.(証明終)
自然数の集合が可算であることは自明です.しかし,A君の証明も正しいように思えます.実際,私はその場で証明の間違い指摘することができず,「面白いことを考えますねぇ」,「不思議ですねぇ」,「どうしてでしょうねぇ」,「後でじっくり考えてみましょう」などとお茶を濁し,そのまま講義室を後にしました.
講義から4時間ほど経った午後8時過ぎ.ある会合の懇親会に出席した私は,大学周辺を千鳥足で歩きながら,もう一度A君の証明を考えました.適度にお酒を飲んでリラックスしていたのがよかったのでしょう.自宅に着く前に証明の間違いに気がつきました.
【私の回答】A君の方法で各自然数を無限列に変換すると,どの無限列にもある有限の数kが存在して,右からk番目の数字は0でなく,それより左の数字はすべて0となります.一方,無限列...111112においては右端を除いてすべて1ですので,そのような有限の数kは存在しません.このことは無限列...111112がどの自然数にも対応しないことを意味します.したがって,この無限列が上の表に存在しなくても矛盾は導かれません.(回答終)
A君いかがでしょうか?
(2014/12/19公開)
エルデシュ数
ハンガリー出身の数学者ポール・エルデシュ(Paul Erdős, 1913-1996)は生涯に約1500本もの論文を発表しました.そのうち507本が共著論文であり,彼の共著者は511人に上るそうです.その共著者の多さに着目して考案されたのがエルデシュ数です.これは次のように定義されます.まず,エルデシュ自身のエルデシュ数を0とします.次にエルデシュの共著者511人のエルデシュ数を1とします.あとはnを1以上の整数として,エルデシュ数nの人との共著論文があり,エルデシュ数n未満の人との共著論文がない人のエルデシュ数をn+1とします.例えば,エルデシュとの共著論文はないがエルデシュの共著者との共著論文がある人のエルデシュ数は2となります.エルデシュ数のことは以前から知っていたのですが,私には関係ないとずっと思っていました.ところがある日,エルデシュ数が2以下の科学者の一覧(Erdős Number Project で公開されています)を何気なく眺めていたところ,私につながりそうな人の名前を見つけました.うれしくなって更に調べてみると,確かに下記4本の論文で Erdős から私につながっていることがわかりました.
- P. Diaconis and P. Erdős, “On the distribution of the greatest common divisor,” Technical Report, Stanford University, 1997.
この論文は Lecture Notes-Monograph Series (2004) に再掲載されているようです. - S. Boyd, P. Diaconis and L. Xiao, “Fastest mixing Markov chain on a graph,” SIAM Review, vol.46, no.4, pp.667-689, 2004.
DOI: 10.1137/S0036144503423264 - S. Boyd and L.O. Chua, “Uniqueness of a basic nonlinear structure,” IEEE Transaction on Circuits and Systems, vol.30, no.9, pp.648-651, 1983.
DOI: 10.1109/TCS.1983.1085403 - N. Takahashi and L.O. Chua, “A New Sufficient Condition for Nonsymmetric CNNs to Have a Stable Equilibrium Point,” IEEE Transactions on Circuits and Systems-I, vol.44, no.11, pp.1092-1095, November 1997.
DOI: 10.1109/81.641777
(2014/11/8公開,2021/6/18リンク修正)
3D画像
2010年が3D元年と呼ばれていることに象徴されるように,3D映像技術がこの数年で急激に普及しました.そこで平成23年度の電気情報工学入門では,3D画像をテーマに掲げ,配属された学生さん達にアナグリフ(赤青メガネ)方式の3D画像を制作してもらいました.使用する機材はデジタルカメラ1台(3D機能はついていません)とノートパソコン1台のみです.1台のデジタルカメラで対象物の写真を2枚(右目用と左目用)撮り,ノートパソコンに取り込んで画像処理ソフトGimpで色と位置の調整をする,という簡単な方法でしたが,予想以上にいい作品ができました.学生さん達の作品の一部を以下に載せておきますので,赤青メガネをお持ちの方はお楽しみ下さい.


(2011/8/12公開)