[ Japanese | English ]
岡山大学 大学院環境生命自然科学研究科 計算機科学講座 / 工学部 情報・電気・数理データサイエンス系 情報工学コース
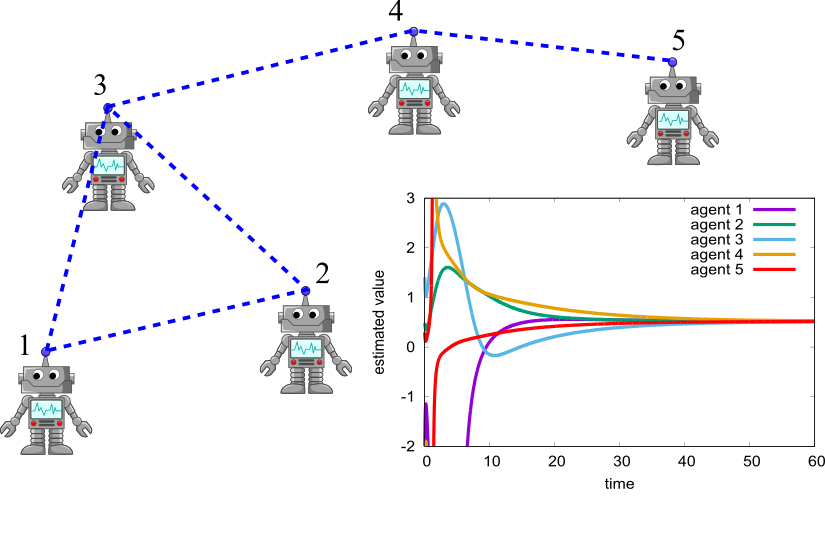
ネットワークを形成する複数の主体(エージェント)による分散計算に大きな注目が集まっており,センサーネットワークにおける情報処理,群ロボットによる協調作業,ニューラルネットワークによる分散学習への応用が期待されています.本研究では,各エージェントが近傍の少数のエージェントとのみ通信可能な状況で,全エージェントが効率的に問題を解決するための方法を開発しています.例えば,全エージェントの状態値の統計量推定,ネットワークの連結度計算,大規模連立一次方程式の解法,主成分分析や非負値行列因子分解の計算法,ニューラルネットワークの分散学習について,理論と数値実験の両面から研究を進めています.これまでの成果をまとめた論文はIEEE Control Systems Lettersなどに掲載されています.
キーワード: マルチエージェントシステム,合意形成,分散計算,分散学習
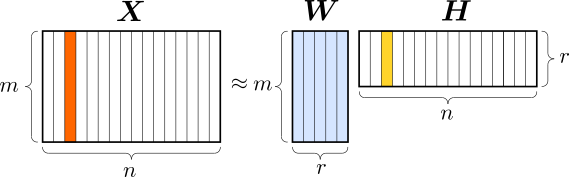
非負値行列因子分解(Nonnegative Matrix Factorization: NMF)は,与えられた非負値データの特徴を抽出する手法であり,顔画像処理,遺伝子解析,テキストマイニング,音楽分類などの幅広い分野で利用されています.本研究では,NMFの効率的計算法として広く利用されている乗法型更新や階層的交互最小二乗法の大域収束性の解析や更なる効率化を行っています. これまでの成果をまとめた論文は国際学術誌Computational Optimization and Applicationsなどに掲載されています.
キーワード: 非負値行列因子分解,特徴抽出,最適化アルゴリズム,大域収束性
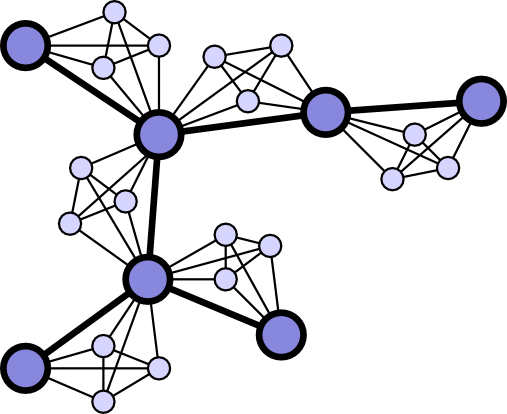
インターネット,World Wide Web,電力線網,友人関係のネットワーク,神経回路網,遺伝子ネットワークなど,現実社会には大規模かつ複雑なネットワークが数多く存在します.それらのネットワークに共通してみられる構造的特徴,形成過程,情報・信号の伝搬機構等を解明することを目標として,近年,多くの研究者が精力的に研究を行っています.本研究では,ネットワークの構造を特徴づける指標である代数的連結度やクラスター係数に着目し,適当な条件の下でそれらの指標を最大または極大にするネットワークを求める問題に取り組んでいます.これまでの成果をまとめた論文は国際学術誌Discrete Applied Mathematics, IEEE Transactions on Control of Network Systemsなどに掲載されています.
キーワード: 複雑ネットワーク,クラスター係数,代数的連結度,グラフ理論
人間は画像中の物体の形等を容易に推定することができるが,無意識下で行われている画像処理過程を数学的に表すことは困難であり,計算機で同様の画像処理を実現する方法は明らかではありません.このような問題に対する一つのアプローチとして,画像生成の物理現象(3次元空間における光の反射等)の逆問題として扱う方法があります.このような技術は生体認証や自動運転の信頼性向上等に重要であると考えられます.これに関する成果は国際会議IW-FCV2021等で発表されています.
キーワード:画像生成モデル,逆問題,最適化

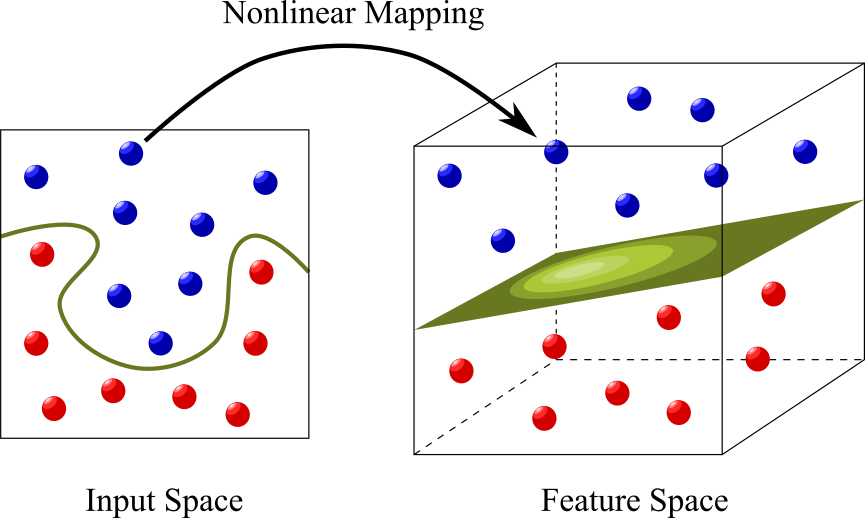
サポートベクトルマシン(Support Vector Machine, SVM)は代表的なパターン識別器の一つであり,その学習は訓練サンプルと同数の変数をもつ凸2次計画問題に帰着されます.本研究では,SVMの学習に現れる大規模凸2次計画問題の効率的解法の一つである分割法の大域収束条件を理論的に導出するとともに,新たな解法を開発しました.これらの成果をまとめた論文は国際論文誌IEEE Transactions on Neural Networksなどに掲載されています.
キーワード:サポートベクトルマシン,パターン識別,回帰,凸2次計画問題
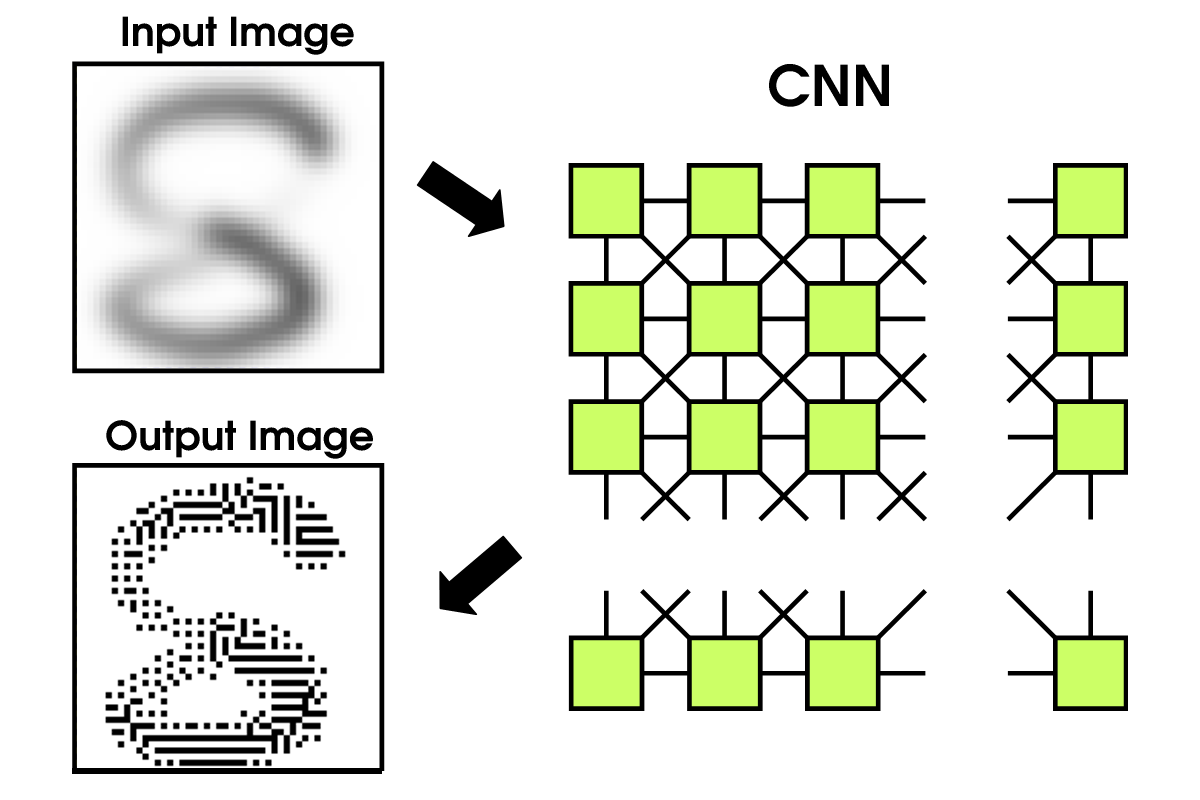
セルラニューラルネットワーク(Cellular Neural Network, CNN) は相互結合型ニューラルネットワークの一種ですが,セルとよばれる基本素子が格子状に配置されている点や,各セルが近傍のセルとのみ結合を有しているという点で他のモデルと区別されます.その構造上の特徴からも分かるように,CNNの主な応用分野は画像処理であり,特に実時間画像処理への応用が期待されています(下図にCNNを用いたハーフトーニングの例を示す).また,結合が局所的であることから集積回路による実装が容易であり,実際,欧州のいくつかの大学でチップが製作されています.本研究では,CNNを用いた信号処理に関する基礎的な課題に取り組んでいます.具体的には,CNNに現れる定常パターン(下図のハーフトーニングの例では出力画像が定常パターンの一つである)の特徴付けや,連想記憶のための最適設計手法に関する研究を行っています.これらの成果をまとめた論文は国際論文誌IEEE Transactions on Circuits and Systems Iなどに掲載されています.
キーワード:セルラニューラルネットワーク,非線形回路,信号処理
人工ニューラルネットワークは人間の脳の神経回路を簡単な形でモデル化したものであり,相互に結合しあった基本素子(ニューロン)が並列・分散的に動作するため,高度な情報処理を高速に実行できると期待されています.本研究では,Hopfieldネットワークを始めとするニューラルネットワーク型非線形システムの大域的な振舞いを理論的に解析し,任意の初期状態に対してネットワークが平衡状態に収束するためのネットワークパラメータに関する条件を導出しました.これらの成果をまとめた論文は国際論文誌IEEE Transactions on Circuits and Systems Iなどに掲載されています.
キーワード:ニューラルネットワーク,非線形力学系,安定性